Historia
de Gauss y como descubrio el campo magnético
Johann
Carl Friedrich Gauss Acerca de este sonido (Gauß) (?·i) (Brunswick, 30 de abril
de 1777 – Gotinga, 23 de febrero de 1855), fue un matemático, astrónomo,
geodesta, y físico alemán que contribuyó significativamente en muchos campos,
incluida la teoría de números, el análisis matemático, la geometría
diferencial, la estadística, el álgebra, la geodesia, el magnetismo y la
óptica. Considerado «el príncipe de las matemáticas» y «el matemático más
grande desde la antigüedad», Gauss ha tenido una influencia notable en muchos
campos de la matemática y de la ciencia, y es considerado uno de los
matemáticos que más influencia ha tenido en la Historia. Fue de los primeros en
extender el concepto de divisibilidad a otros conjuntos.
Gauss
fue un niño prodigio, a pesar de su condición de ser de una familia campesina
de padres analfabetos; de él existen muchas anécdotas acerca de su asombrosa
precocidad. Hizo sus primeros grandes descubrimientos mientras era apenas un
adolescente en el bachillerato y completó su magnum opus, Disquisitiones
arithmeticae a los veintiún años (1798), aunque fue publicado en 1801. Fue un trabajo
fundamental para que se consolidara la teoría de los números y ha moldeado esta
área hasta los días presentes.
Juventud.
Johann
Carl Friedrich Gauss nació en el ducado de Brunswick, Alemania, el 30 de abril
de 1777, en una familia campesina muy pobre: su abuelo era un humilde jardinero
y repartidor. Su padre nunca pudo superar la espantosa miseria con la que
siempre convivió. De pequeño Gauss fue respetuoso y obediente, y ya en su edad
adulta nunca criticó a su padre, quien murió poco después de que Gauss
cumpliera 30 años, por su rudeza y violencia para con él.
Desde
muy pequeño, Gauss mostró su talento para los números y para el lenguaje.
Aprendió a leer solo y, sin que nadie lo ayudara, aprendió muy rápido la
aritmética elemental desde muy pequeño. En 1784, a los siete años de edad,
ingresó a una de las escuelas de primeras letras de Brunswick donde daba clases
un maestro rural llamado Büttner, quien corrigió rápidamente su lectura, le
enseñó gramática, ortografía y caligrafía y perfeccionó su talento matemático y
lo animó a continuar el bachillerato, como consta en su carta para que lo
aceptaran en el Lyceum; pero quien usaba unos métodos severos y una estricta
disciplina, lo que desagradaba a alguien tan sensible. Se cuenta la anécdota de
que, a los dos años de estar en la escuela, durante la clase de Aritmética, el
maestro propuso el problema de sumar los números de una progresión aritmética.1
Gauss halló la respuesta correcta casi inmediatamente diciendo «Ligget se'»
('ya está'). Al acabar la hora se comprobaron las soluciones y se vio que la
solución de Gauss era correcta, mientras que no lo eran muchas de las de sus
compañeros.
Su
pobreza no le hubiera permitido continuar estudiando, pero presentado ante el
duque de Brunswick ingresó al bachillerato bajo su mecenazgo, allí conoció al
matemático Martin Bartels quien fue su profesor y se aceleraron sus progresos
en Matemáticas. Ambos estudiaban juntos, se apoyaban y se ayudaban para
descifrar y entender los manuales que tenían sobre álgebra y análisis
elemental. En estos años se empezaron a gestar algunas de las ideas y formas de
ver las matemáticas, que caracterizaron posteriormente a Gauss. Se dio cuenta,
por ejemplo, del poco rigor en muchas demostraciones de los grandes matemáticos
que le precedieron, como Newton, Euler, Lagrange y otros más.
A
los 12 años ya miraba con cierto recelo los fundamentos de la geometría, y a
los 16 tuvo sus primeras ideas intuitivas sobre la posibilidad de otro tipo de
geometría. A los 17 años, Gauss se dio a la tarea de completar lo que, a su
juicio, habían dejado a medias sus predecesores en materia de teoría de
números. Así descubrió su pasión por la aritmética, área en la que poco después
tuvo sus primeros triunfos. Su gusto por la aritmética prevaleció por toda su vida,
ya que para él «La matemática es la reina de las ciencias y la aritmética es la
reina de las matemáticas». Gauss tenía 14 años cuando conoció al duque de
Brunswick Ferdinand. Este quedó fascinado por lo que había oído del muchacho, y
por su modestia y timidez, por lo que decidió hacerse cargo de todos los gastos
de Gauss para asegurar que su educación llegara a buen fin.
Al
año siguiente de conocer al duque, Gauss ingresó al Collegium Carolinum para
continuar sus estudios, y lo que sorprendió a todos fue su facilidad para las
lenguas. Aprendió y dominó el griego y el latín en muy poco tiempo. Estuvo tres
años en el Collegium y, al salir, no tenía claro si quería dedicarse a las
matemáticas o a la filología. En esta época ya había descubierto su ley de los
mínimos cuadrados, lo que indica el temprano interés de Gauss por la teoría de
errores de observación y su distribución.
Madurez
En
1796 demostró que se puede dibujar un polígono regular de 17 lados con regla y
compás.
Fue
el primero en probar rigurosamente el teorema fundamental del álgebra
(disertación para su tesis doctoral en 1799), aunque una prueba casi completa
de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente.
En
1801 publicó el libro Disquisitiones arithmeticae, con seis secciones dedicadas
a la Teoría de números, dándole a esta rama de las matemáticas una estructura
sistematizada. En la última sección del libro expone su tesis doctoral. Ese
mismo año predijo la órbita de Ceres aproximando parámetros por mínimos
cuadrados.
En
1809 fue nombrado director del Observatorio de Gotinga. En este mismo año
publicó Theoria motus corporum coelestium in sectionibus conicis Solem
ambientium describiendo cómo calcular la órbita de un planeta y cómo refinarla
posteriormente. Profundizó sobre ecuaciones diferenciales y secciones cónicas.
Gauss
murió en Gotinga el 23 de febrero de 1855.
Disquisitiones
arithmeticae.
La
primera estancia de Gauss en Gotinga duró tres años, que fueron de los más
productivos de su vida. Regresó a su ciudad natal Brunswick a finales de 1798
sin haber recibido ningún título en la Universidad, pero en ese momento su
primera obra maestra, Disquisitiones arithmeticae, estaba casi lista aunque no
se publicó por primera vez hasta 1801.
Este
libro, escrito en latín, está dedicado a su mecenas, el duque Ferdinand, por
quien Gauss sentía mucho respeto y agradecimiento. Es un tratado de la teoría
de números en el que se sintetiza y perfecciona todo el trabajo previo en esta
área. La obra consta de 8 capítulos pero el octavo no se pudo imprimir por
cuestiones financieras. El teorema fundamental del álgebra establece que un
polinomio en una variable, no constante y a coeficientes complejos, tiene
tantas raíces como su grado.
Contribuciones
a la Teoría del Potencial.
El
Teorema de la divergencia de Gauss, de 1835 y publicado apenas en 1867, es
fundamental para la teoría del potencial y la física. Coloca en un campo
vectorial la integral del volumen para la divergencia de un campo vectorial en
relación con la integral de superficie del campo vectorial alrededor de dicho
volumen.
Magnetismo.
1831
será un año clave en la vida de Gauss. Si un año antes su hijo Eugen emigra a
Estados Unidos al parecer por desavenencias familiares, este año muere Minna la
segunda esposa de Gauss. Desde entonces será su hija Therèse la que se
encargará de los asuntos domésticos.
Pero a finales de ese año llega a Gottingën
Wilhelm Weber, para ocupar la plaza de profesor de Física. A partir de este momento
un decaído Gauss va a encontrar otra vez en la ciencia la solución de sus males
familiares.
Gauss y WeberEn estrecha colaboración con
Weber Gauss desarrollará una intensa labor en el estudio del magnetismo
terrestre. Acoge con entusiasmo la propuesta de Alexander von Humbodlt de crear
una red de observatorios magnéticos que cubran toda la superficie terrestre.
En la década de los 30 publica varias obras
sobre el tema: Intensitas vis magneticae terrestris ad mensuram absolutam
revocata (1832), que trata teorías actuales sobre magnetismo terrestre,
anticipando las ideas de Poisson, la medida absoluta de la fuerza magnética y
una definición empírica del magnetismo terrestre, Allgemeine Theorie Erdmagnetismus (1839), en
la que demuestra que solo puede haber dos polos y sienta las bases para
determinar la intensidad de la componente horizontal de la fuerza magnética
junto con el ángulo de inclinación. Se ayuda de la ecuación de Laplace y
especifica la ubicación del polo sur magnético.
Ambos
construyen el primer telégrafo electromagnético que conseguía transmitir hasta
nueve letras por minuto a una distancia de 500 pies, la que se paraba el
Observatorio Astronómico de la Facultad de Física.
Junto a Weber es autor del primer atlas
geomagnético terrestre y de más de 40 obras sobre mediciones magnéticas de la
Sociedad de Magnetismo, fundada por ellos, y de nuevas herramientas para medir
el campo magnético.
Sin embargo, un hecho va a truncar esta
fructífera colaboración, Weber, junto a otros 6 profesores, es despedido de su
cargo por negarse a jurar fidelidad al nuevo rey Ernesto Augusto von
Cumberland, que había derogado la constitución de 1833. Gauss, de carácter
conservador, no movería un dedo a pesar de su influencia para detener el
despido, a pesar de que entre los 7 de Gottingën estaban su propio yerno y su
inseparable colaborador.
Tras la marcha definitiva de Weber de
Gottingën la producción científica de Gauss disminuye de forma rotunda. Trabaja
en sus observaciones astronómicas, en dióptrica, en la teoría del potencial, en
geodesia pero todas son obras menores.
Ley de Gauss del campo magnético
En
física la ley de Gauss establece que el flujo de ciertos campos a través de una
superficie cerrada es proporcional a la magnitud de las fuentes de dicho campo
que hay en el interior de dicha superficie. Dichos campos son aquellos cuya
intensidad decrece como la distancia a la fuente al cuadrado. La constante de
proporcionalidad depende del sistema de unidades empleado.
Se
aplica al campo electrostático y al gravitatorio. Sus fuentes son la carga
eléctrica y la masa, respectivamente. También puede aplicarse al campo
magnetostático.
André-Marie Ampère
(Lyon,
1775-Marsella, 1836) Físico francés. Fundador de la actual disciplina de la
física conocida como electromagnetismo, ya en su más pronta juventud destacó
como prodigio; a los doce años estaba familiarizado, de forma autodidacta, con
todas las matemáticas conocidas en su tiempo. En 1801 ejerció como profesor de
física y química en Bourg-en-Bresse, y posteriormente en París, en la École
Centrale. Impresionado por su talento, Napoleón lo promocionó al cargo de
inspector general del nuevo sistema universitario francés, puesto que desempeñó
hasta el final de sus días.
El
talento de Ampère no residió tanto en su capacidad como experimentador metódico
como en sus brillantes momentos de inspiración: en 1820, el físico danés Hans
Christian Oersted experimentó las desviaciones en la orientación que sufre una
aguja imantada cercana a un conductor de corriente eléctrica, hecho que de modo
inmediato sugirió la interacción entre electricidad y magnetismo; en sólo una
semana, Ampère fue capaz de elaborar una amplia base teórica para explicar este
nuevo fenómeno.
Esta
línea de trabajo le llevó a formular una ley empírica del electromagnetismo,
conocida como ley de Ampère (1825), que describe matemáticamente la fuerza
magnética existente entre dos corrientes eléctricas. Algunas de sus
investigaciones más importantes quedaron recogidas en su Colección de
observaciones sobre electrodinámica (1822) y su Teoría de los fenómenos
electromagnéticos (1826).
Su
desarrollo matemático de la teoría electromagnética no sólo sirvió para
explicar hechos conocidos con anterioridad, sino también para predecir nuevos
fenómenos todavía no descritos en aquella época. No sólo teorizó sobre los
efectos macroscópicos del electromagnetismo, sino que además intentó construir
un modelo microscópico que explicara toda la fenomenología electromagnética,
basándose en la teoría de que el magnetismo es debido al movimiento de cargas
en la materia (adelantándose mucho a la posterior teoría electrónica de la
materia). Además, fue el primer científico que sugirió cómo medir la corriente:
mediante la determinación de la desviación sufrida por un imán al paso de una
corriente eléctrica (anticipándose de este modo al galvanómetro).
Ley de Ampere
En
física del magnetismo, la ley de Ampère, modelada por André-Marie Ampère en
1831,1 relaciona un campo magnético estático con la causa que la produce, es
decir, una corriente eléctrica estacionaria. James Clerk Maxwell la corrigió
posteriormente y ahora es una de las ecuaciones de Maxwell, formando parte del
electromagnetismo de la física clásica.
La
ley de Ampére explica, que la circulación de la intensidad del campo magnético
en un contorno cerrado es igual a la corriente que lo recorre en ese contorno.
El
campo magnético es un campo angular con forma circular, cuyas líneas encierran
la corriente. La dirección del campo en un punto es tangencial al círculo que
encierra la corriente.
El
campo magnético disminuye inversamente con la distancia al conductor.
Michael Faraday.
(Newington,
Gran Bretaña, 1791-Londres, 1867) Científico británico. Uno de los físicos más
destacados del siglo XIX, nació en el seno de una familia humilde y recibió una
educación básica. A temprana edad tuvo que empezar a trabajar, primero como
repartidor de periódicos, y a los catorce años en una librería, donde tuvo la
oportunidad de leer algunos artículos científicos que lo impulsaron a realizar
sus primeros experimentos.
Tras
asistir a algunas conferencias sobre química impartidas por sir Humphry Davy en
la Royal Institution, Faraday le pidió que lo aceptara como asistente en su
laboratorio. Cuando uno de sus ayudantes dejó el puesto, Davy se lo ofreció a
Faraday. Pronto se destacó en el campo de la química, con descubrimientos como
el benceno y las primeras reacciones de sustitución orgánica conocidas, en las
que obtuvo compuestos clorados de cadena carbonada a partir de etileno.
En
esa época, el científico danés Hans Christian Oersted descubrió los campos
magnéticos generados por corrientes eléctricas. Basándose en estos
experimentos, Faraday logró desarrollar el primer motor eléctrico conocido. En
1831 colaboró con Charles Wheatstone e investigó sobre fenómenos de inducción
electromagnética. Observó que un imán en movimiento a través de una bobina
induce en ella una corriente eléctrica, lo cual le permitió describir
matemáticamente la ley que rige la producción de electricidad por un imán.
Realizó
además varios experimentos electroquímicos que le permitieron relacionar de
forma directa materia con electricidad. Tras observar cómo se depositan las
sales presentes en una cuba electrolítica al pasar una corriente eléctrica a su
través, determinó que la cantidad de sustancia depositada es directamente proporcional
a la cantidad de corriente circulante, y que, para una cantidad de corriente
dada, los distintos pesos de sustancias depositadas están relacionados con sus
respectivos equivalentes químicos.
Posteriores
aportaciones que resultaron definitivas para el desarrollo de la física, como
es el caso de la teoría del campo electromagnético introducida por James Clerk
Maxwell, se fundamentaron en la labor pionera que había llevado a cabo Michael
Faraday.
Ley de Faraday
La ley de inducción electromagnética
de Faraday (o simplemente ley de Faraday) establece que
el voltaje inducido en un circuito cerrado es directamente proporcional a
la rapidez con que cambia en el tiempo el flujo magnético que atraviesa una superficie cualquiera con el circuito como borde:
Esta ley fue formulada a
partir de los experimentos que Michael
Faraday realizó en 1831. Esta ley tiene importantes
aplicaciones en la generación de
electricidad.
Heinrich Friedrich Emil Lenz
(Dorpat,
1804 - Roma, 1865) Físico ruso. Profesor y rector de la Universidad de San
Petersburgo, estudió el efecto Peltier, la conductividad de los metales y la
variación de la resistencia eléctrica con la temperatura. Enunció una ley que
permite conocer la dirección y el sentido de la corriente inducida en un
circuito eléctrico.
Estudió
física y química en la Universidad de Dorpat y, muy joven aún, tomo parte como
geofísico en una expedición alrededor del mundo, durante la cual efectuó
mediciones sobre el nivel de sal, la temperatura y la presión de mares y
océanos. Afincado luego en San Petersburgo, ejerció la docencia en la
Universidad y en la Academia de Ciencias de esta ciudad, de la que llegaría a
ser decano y rector.
Lenz
estudió la conductividad eléctrica y descubrió el efecto conocido como efecto
Joule con independencia de las experiencias y conclusiones a que a este
respecto llegó el científico que le dio nombre. La ley de Lenz, enunciada en
1833, fue la gran aportación de Heinrich Lenz a los estudios electromagnéticos;
esta ley permite determinar el sentido de la corriente inducida por una
variación del flujo abarcado por un circuito.
Para
generar una corriente eléctrica es preciso realizar un trabajo mecánico o bien,
de algún modo, desarrollar una energía. Por lo tanto, de acuerdo con el
principio de la conservación de la energía, la corriente generada constituirá
una resistencia que hay que vencer. La ley de Lenz expresa esto diciendo que el
sentido de la corriente inducida es tal que tiende a oponerse a la causa que la
provoca. Así, al acercar un imán a una espira, la corriente inducida que
aparece en ésta tiene un sentido de circulación tal que crea un campo magnético
que repele el imán. Por otro lado, al separar el imán, la corriente inducida
será ahora opuesta a la anterior y atraerá el imán.
Ley de Lenz.
La
ley de Lenz para el campo electromagnético relaciona cambios producidos en el
campo eléctrico en un conductor con la variación de flujo magnético en dicho
conductor, y afirma que las tensiones o voltajes inducidos sobre un conductor y
los campos eléctricos asociados son de un sentido tal que se oponen a la
variación del flujo magnético que las induce. Esta ley se llama así en honor
del físico germano-báltico Heinrich Lenz, quien la formuló en el año 1834. En
un contexto más general que el usado por Lenz, se conoce que dicha ley es una
consecuencia más del principio de conservación de la energía aplicado a la
energía del campo electromagnético.
La
polaridad de una tensión inducida es tal, que tiende a producir una corriente,
cuyo campo magnético se opone siempre a las variaciones del campo existente
producido por la corriente original.
El
flujo de un campo magnético uniforme a través de un circuito plano viene dado
por:
Si el conductor está en movimiento el valor del flujo será:
A su vez, el valor del
flujo puede variar debido a un cambio en el valor del campo magnético:
En este caso la Ley de Faraday afirma que la tensión inducida ℰ en cada instante tiene
por valor:
Donde ℰ es el voltaje
inducido y dΦ/dt es la tasa de variación temporal del
flujo magnético Φ. La
dirección voltaje inducido(el signo negativo en la fórmula) se debe a la
oposición al cambio de flujo magnético.
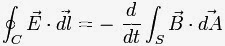




No hay comentarios.:
Publicar un comentario